pacman::p_load(sf, sfdep, tmap, tidyverse, knitr, plotly, zoo, Kendall, spdep)Take-home-project
Geospatial Proj
Getting Started
Lets make make sure that sfdep, sf, tmap and tidyverse packages of R are currently installed
Importing OD data into R
Firstly we will import the Passenger volume by Origin Destination Bus Stops data set downloaded from LTA DataMall by using read_csv() of readr package.
odbus <- read_csv("data/aspatial/origin_destination_bus_202308.csv")
glimpse(odbus)Rows: 5,709,512
Columns: 7
$ YEAR_MONTH <chr> "2023-08", "2023-08", "2023-08", "2023-08", "2023-…
$ DAY_TYPE <chr> "WEEKDAY", "WEEKENDS/HOLIDAY", "WEEKENDS/HOLIDAY",…
$ TIME_PER_HOUR <dbl> 16, 16, 14, 14, 17, 17, 17, 17, 7, 17, 14, 10, 10,…
$ PT_TYPE <chr> "BUS", "BUS", "BUS", "BUS", "BUS", "BUS", "BUS", "…
$ ORIGIN_PT_CODE <chr> "04168", "04168", "80119", "80119", "44069", "4406…
$ DESTINATION_PT_CODE <chr> "10051", "10051", "90079", "90079", "17229", "1722…
$ TOTAL_TRIPS <dbl> 7, 2, 3, 10, 5, 4, 3, 22, 3, 3, 7, 1, 3, 1, 3, 1, …Origin & Destination Bus Stop Code
odbus$ORIGIN_PT_CODE <-
as.factor(odbus$ORIGIN_PT_CODE)
odbus$DESTINATION_PT_CODE <-
as.factor(odbus$DESTINATION_PT_CODE)Extracting study data
We will filter out the data according to the requirements set out by Professor 1.) “Weekday @ 6-9am”
origtrip_6_9 <- odbus %>%
filter(DAY_TYPE == "WEEKDAY") %>%
filter(TIME_PER_HOUR >= 6 &
TIME_PER_HOUR <= 9) %>%
group_by(ORIGIN_PT_CODE) %>%
summarise(TRIPS = sum(TOTAL_TRIPS))Writing the data to RDS
kable(head(origtrip_6_9))| ORIGIN_PT_CODE | TRIPS |
|---|---|
| 01012 | 1973 |
| 01013 | 952 |
| 01019 | 1789 |
| 01029 | 2561 |
| 01039 | 2938 |
| 01059 | 1651 |
write_rds(origtrip_6_9, "data/rds/origtrip_6_9.rds")2.) “Weekday @ 5-8pm”
origtrip_17_20 <- odbus %>%
filter(DAY_TYPE == "WEEKDAY") %>%
filter(TIME_PER_HOUR >= 17 &
TIME_PER_HOUR <= 20) %>%
group_by(ORIGIN_PT_CODE) %>%
summarise(TRIPS = sum(TOTAL_TRIPS))
glimpse(origtrip_17_20)Rows: 5,035
Columns: 2
$ ORIGIN_PT_CODE <fct> 01012, 01013, 01019, 01029, 01039, 01059, 01109, 01112,…
$ TRIPS <dbl> 8448, 7328, 3608, 9317, 12937, 2133, 322, 45010, 27233,…Writing the data to RDS
kable(head(origtrip_17_20))| ORIGIN_PT_CODE | TRIPS |
|---|---|
| 01012 | 8448 |
| 01013 | 7328 |
| 01019 | 3608 |
| 01029 | 9317 |
| 01039 | 12937 |
| 01059 | 2133 |
write_rds(origtrip_17_20, "data/rds/origtrip_17_20.rds")3.) “Weekend @ 11am-2pm”
origtrip_11_14 <- odbus %>%
filter(DAY_TYPE == "WEEKENDS/HOLIDAY") %>%
filter(TIME_PER_HOUR >= 11 &
TIME_PER_HOUR <= 14) %>%
group_by(ORIGIN_PT_CODE) %>%
summarise(TRIPS = sum(TOTAL_TRIPS))Writing the data to RDS
kable(head(origtrip_11_14))| ORIGIN_PT_CODE | TRIPS |
|---|---|
| 01012 | 2273 |
| 01013 | 1697 |
| 01019 | 1511 |
| 01029 | 3272 |
| 01039 | 5424 |
| 01059 | 1062 |
write_rds(origtrip_11_14, "data/rds/origtrip_11_14.rds")4.) “Weekend @ 4-7pm”
origtrip_16_19 <- odbus %>%
filter(DAY_TYPE == "WEEKENDS/HOLIDAY") %>%
filter(TIME_PER_HOUR >= 16 &
TIME_PER_HOUR <= 19) %>%
group_by(ORIGIN_PT_CODE) %>%
summarise(TRIPS = sum(TOTAL_TRIPS))Writing the data to RDS
kable(head(origtrip_16_19))| ORIGIN_PT_CODE | TRIPS |
|---|---|
| 01012 | 3208 |
| 01013 | 2796 |
| 01019 | 1623 |
| 01029 | 4244 |
| 01039 | 7403 |
| 01059 | 1190 |
write_rds(origtrip_16_19, "data/rds/origtrip_16_19.rds")Reading each RDS file
origtrip_11_14 <- read_rds("data/rds/origtrip_11_14.rds")
origtrip_16_19 <- read_rds("data/rds/origtrip_16_19.rds")
origtrip_17_20 <- read_rds("data/rds/origtrip_17_20.rds")
origtrip_6_9 <- read_rds("data/rds/origtrip_6_9.rds")Importing geospatial data
busstop <- st_read(dsn = "data/geospatial",
layer = "BusStop") %>%
st_transform(crs = 3414)Reading layer `BusStop' from data source
`/Users/youting/ytquek/ISSS624/Project/data/geospatial' using driver `ESRI Shapefile'
Simple feature collection with 5161 features and 3 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 3970.122 ymin: 26482.1 xmax: 48284.56 ymax: 52983.82
Projected CRS: SVY21Glimpse the Bus Stop tibble data frame
glimpse(busstop)Rows: 5,161
Columns: 4
$ BUS_STOP_N <chr> "22069", "32071", "44331", "96081", "11561", "66191", "2338…
$ BUS_ROOF_N <chr> "B06", "B23", "B01", "B05", "B05", "B03", "B02A", "B02", "B…
$ LOC_DESC <chr> "OPP CEVA LOGISTICS", "AFT TRACK 13", "BLK 239", "GRACE IND…
$ geometry <POINT [m]> POINT (13576.31 32883.65), POINT (13228.59 44206.38),…Load Map into MPSZ
mpsz <- st_read(dsn = "data/geospatial",
layer = "MPSZ-2019") %>%
st_transform(crs = 3414)Reading layer `MPSZ-2019' from data source
`/Users/youting/ytquek/ISSS624/Project/data/geospatial' using driver `ESRI Shapefile'
Simple feature collection with 332 features and 6 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: 103.6057 ymin: 1.158699 xmax: 104.0885 ymax: 1.470775
Geodetic CRS: WGS 84glimpse(mpsz)Rows: 332
Columns: 7
$ SUBZONE_N <chr> "MARINA EAST", "INSTITUTION HILL", "ROBERTSON QUAY", "JURON…
$ SUBZONE_C <chr> "MESZ01", "RVSZ05", "SRSZ01", "WISZ01", "MUSZ02", "MPSZ05",…
$ PLN_AREA_N <chr> "MARINA EAST", "RIVER VALLEY", "SINGAPORE RIVER", "WESTERN …
$ PLN_AREA_C <chr> "ME", "RV", "SR", "WI", "MU", "MP", "WI", "WI", "SI", "SI",…
$ REGION_N <chr> "CENTRAL REGION", "CENTRAL REGION", "CENTRAL REGION", "WEST…
$ REGION_C <chr> "CR", "CR", "CR", "WR", "CR", "CR", "WR", "WR", "CR", "CR",…
$ geometry <MULTIPOLYGON [m]> MULTIPOLYGON (((33222.98 29..., MULTIPOLYGON (…Geospatial Data Wrangling
Combining Busstop and mpsz
busstop_mpsz <- st_intersection(busstop, mpsz) %>%
select(BUS_STOP_N, SUBZONE_C) %>%
st_drop_geometry()
glimpse(busstop_mpsz)Rows: 5,156
Columns: 2
$ BUS_STOP_N <chr> "13099", "13089", "06151", "13211", "13139", "13109", "1311…
$ SUBZONE_C <chr> "RVSZ05", "RVSZ05", "SRSZ01", "SRSZ01", "SRSZ01", "SRSZ01",…write_rds(busstop_mpsz, "data/rds/busstop_mpsz.csv") origin_6_9 <- left_join(origtrip_6_9 , busstop_mpsz,
by = c("ORIGIN_PT_CODE" = "BUS_STOP_N")) %>%
rename(ORIGIN_BS = ORIGIN_PT_CODE,
ORIGIN_SZ = SUBZONE_C) %>%
group_by(ORIGIN_SZ) %>%
summarise(TOT_TRIPS = sum(TRIPS))
glimpse(origin_6_9)Rows: 312
Columns: 2
$ ORIGIN_SZ <chr> "AMSZ01", "AMSZ02", "AMSZ03", "AMSZ04", "AMSZ05", "AMSZ06", …
$ TOT_TRIPS <dbl> 116600, 226521, 199437, 114549, 70770, 102390, 23231, 28011,…origin_17_20 <- left_join(origtrip_17_20 , busstop_mpsz,
by = c("ORIGIN_PT_CODE" = "BUS_STOP_N")) %>%
rename(ORIGIN_BS = ORIGIN_PT_CODE,
ORIGIN_SZ = SUBZONE_C) %>%
group_by(ORIGIN_SZ) %>%
summarise(TOT_TRIPS = sum(TRIPS))origin_11_14 <- left_join(origtrip_11_14 , busstop_mpsz,
by = c("ORIGIN_PT_CODE" = "BUS_STOP_N")) %>%
rename(ORIGIN_BS = ORIGIN_PT_CODE,
ORIGIN_SZ = SUBZONE_C) %>%
group_by(ORIGIN_SZ) %>%
summarise(TOT_TRIPS = sum(TRIPS))origin_16_19 <- left_join(origtrip_16_19 , busstop_mpsz,
by = c("ORIGIN_PT_CODE" = "BUS_STOP_N")) %>%
rename(ORIGIN_BS = ORIGIN_PT_CODE,
ORIGIN_SZ = SUBZONE_C) %>%
group_by(ORIGIN_SZ) %>%
summarise(TOT_TRIPS = sum(TRIPS))Setting up the Hexagon Grid
Drawing the Hexagon Grid
Drawing the hexagon grid over the mpsz map
area_honeycomb_grid = st_make_grid(mpsz, c(500), what = "polygons", square = FALSE)To sf and add grid ID
honeycomb_grid_sf = st_sf(area_honeycomb_grid) %>%
mutate(grid_id = 1:length(lengths(area_honeycomb_grid)))busstop_honeycomb <- st_intersection(honeycomb_grid_sf,busstop) %>%
select(BUS_STOP_N, grid_id) %>%
st_drop_geometry()write_rds(busstop_honeycomb, "data/rds/busstop_honeycomb.csv")duplicate <- busstop_honeycomb %>%
group_by_all() %>%
filter(n()>1) %>%
ungroup()busstop_honeycomb <- unique(busstop_honeycomb)Filter grid without values or a grid_id (i.e. no points in side that grid)
busstop_honeycomb <- busstop_honeycomb %>%
filter(!is.na(grid_id) & grid_id > 0)Assign every Bus Stop with a Grid ID
origin_6_9 <- left_join(busstop_honeycomb, origtrip_6_9,
by = c("BUS_STOP_N" = "ORIGIN_PT_CODE"))
origin_6_9 <- origin_6_9 %>%
filter(!is.na(TRIPS) & TRIPS > 0)
origin_17_20 <- left_join(busstop_honeycomb, origtrip_17_20,
by = c("BUS_STOP_N" = "ORIGIN_PT_CODE"))
origin_17_20 <- origin_17_20 %>%
filter(!is.na(TRIPS) & TRIPS > 0)
origin_11_14 <- left_join(busstop_honeycomb, origtrip_11_14,
by = c("BUS_STOP_N" = "ORIGIN_PT_CODE"))
origin_11_14 <- origin_11_14 %>%
filter(!is.na(TRIPS) & TRIPS > 0)
origin_16_19 <- left_join(busstop_honeycomb, origtrip_16_19,
by = c("BUS_STOP_N" = "ORIGIN_PT_CODE"))
origin_16_19 <- origin_16_19 %>%
filter(!is.na(TRIPS) & TRIPS > 0)Choropleth Visualisation
Weekday Morning Peak 6am-9am
total_trips_by_grid_6_9 <- origin_6_9 %>%
group_by(grid_id) %>%
summarise(total_trips = sum(TRIPS, na.rm = TRUE))Merge geospatial data
total_trips_by_grid_6_9 <- total_trips_by_grid_6_9 %>%
left_join(honeycomb_grid_sf, by = c("grid_id" = "grid_id"))
total_trips_by_grid_sf_6_9 <- st_sf(total_trips_by_grid_6_9)Plot the Choropleth map
tmap_mode("view")
tm_shape(total_trips_by_grid_sf_6_9) +
tm_fill(
col = "total_trips",
palette = "Reds",
style = "cont",
title = "Total Trips Taken - Weekday Morning Peak 6-9am",
id = "grid_id",
showNA = FALSE,
alpha = 0.6,
popup.vars = c(
"Number of trips: " = "total_trips"
),
popup.format = list(
total_trips = list(format = "f", digits = 0)
)
) +
tm_borders(col = "grey40", lwd = 0.4)Weekday Afternoon Peak 5pm - 8pm
total_trips_by_grid_17_20 <- origin_17_20 %>%
group_by(grid_id) %>%
summarise(total_trips = sum(TRIPS, na.rm = TRUE))Merge geospatial data
total_trips_by_grid_17_20 <- total_trips_by_grid_17_20 %>%
left_join(honeycomb_grid_sf, by = c("grid_id" = "grid_id"))
total_trips_by_grid_sf_17_20 <- st_sf(total_trips_by_grid_17_20)Plot the Choropleth map
tmap_mode("view")
tm_shape(total_trips_by_grid_sf_17_20) +
tm_fill(
col = "total_trips",
palette = "Reds",
style = "cont",
title = "Total Trips Taken - Weekday Afternoon Peak 5 - 8 pm",
id = "grid_id",
showNA = FALSE,
alpha = 0.6,
popup.vars = c(
"Number of trips: " = "total_trips"
),
popup.format = list(
total_trips = list(format = "f", digits = 0)
)
) +
tm_borders(col = "grey40", lwd = 0.4)Weekday/Weekend Morning Peak 11am-2pm
total_trips_by_grid <- origin_11_14 %>%
group_by(grid_id) %>%
summarise(total_trips = sum(TRIPS, na.rm = TRUE))Merge geospatial data
total_trips_by_grid <- total_trips_by_grid %>%
left_join(honeycomb_grid_sf, by = c("grid_id" = "grid_id"))
total_trips_by_grid_sf <- st_sf(total_trips_by_grid)Plot the Choropleth map
tmap_mode("view")
tm_shape(total_trips_by_grid_sf) +
tm_fill(
col = "total_trips",
palette = "Reds",
style = "cont",
title = "Total Trips Taken - Weekday Morning Peak 6-9am",
id = "grid_id",
showNA = FALSE,
alpha = 0.6,
popup.vars = c(
"Number of trips: " = "total_trips"
),
popup.format = list(
total_trips = list(format = "f", digits = 0)
)
) +
tm_borders(col = "grey40", lwd = 0.4)Weekend/Holiday Peak 4pm-7pm
total_trips_by_grid <- origin_16_19 %>%
group_by(grid_id) %>%
summarise(total_trips = sum(TRIPS, na.rm = TRUE))Merge geospatial data
total_trips_by_grid <- total_trips_by_grid %>%
left_join(honeycomb_grid_sf, by = c("grid_id" = "grid_id"))
total_trips_by_grid_sf <- st_sf(total_trips_by_grid)Plot the Choropleth map
tmap_mode("view")
tm_shape(total_trips_by_grid_sf) +
tm_fill(
col = "total_trips",
palette = "Reds",
style = "cont",
title = "Total Trips Taken - Weekend Morning Peak 4-7pm",
id = "grid_id",
showNA = FALSE,
alpha = 0.6,
popup.vars = c(
"Number of trips: " = "total_trips"
),
popup.format = list(
total_trips = list(format = "f", digits = 0)
)
) +
tm_borders(col = "grey40", lwd = 0.4)Summary of our data analysis
From a data analysis point of view, we see that there is a huge fluctuations in the 4 time spaces of Bus Trips. Starting from Weekday Morning 6 to 9 am with a peak of near 300k trips all the way till Weekday Afternoon 5-8pm of 500k.
Towards the weekend, the numbers start to scale back significantly to a peak of 100k indicating citizens of Singapore are less likely to travel by the bus during the weekends.
Local Indicators of Spatial Association (LISA) Analysis
Introduction
We will use the a Moran I function to compute a z-score, a pseudo p-value, and a code representing the cluster type for each statistically significant feature.
Computing Contiguity Spatial Weights
Below are the steps to do so
Step 1 Check for null Neighbours
# Check for empty neighbor sets
empty_neighbors <- which(sapply(total_trips_by_grid_sf, length) == 0)
# Print the indices of observations with no neighbors
if (length(empty_neighbors) > 0) {
cat("Observations with no neighbors:", empty_neighbors, "\n")
} else {
cat("All observations have at least one neighbor.\n")
}All observations have at least one neighbor.Step 2 Create a list of all neighbours
# Create neighbor list
wm08 <- total_trips_by_grid_sf %>%
mutate(nb = st_contiguity(area_honeycomb_grid))
# Filter out observations where 'nb' contains the value 0
# Assuming '0' is an unwanted value in the 'nb' list
wm08 <- wm08 %>%
filter(!sapply(nb, function(x) any(x == 0)))
# Now, you can proceed with creating the weights
wm08 <- wm08 %>%
mutate(
wt = st_weights(nb, style = "W"),
.before = 1
)Step 3 Plot a map based on the list of neighbours
# Set map to static
tmap_mode("view")
map_08 <- tm_shape(wm08) +
tm_fill(
col = "total_trips",
palette = "PuRd",
style = "pretty",
title = "Trip sizes"
) +
tm_layout(main.title = "Total Bus Trips Across the Island ",
main.title.size = 1,
main.title.position = "center",
legend.position = c("left", "top"),
legend.height = .6,
legend.width = .2,
frame = FALSE
)
map_08Step 4 : Calculate the Moran values using local_moran function
For sanity purposes, we will fold the other timezones (weekday & weekday afternoon) code other than the first dataframe for Weekday Morning.
The local_moran functions will append the below variables for our assessment later.
| Variable | Description |
|---|---|
| var_ii (Variance of Ii): | The variability of the Moran’s I simulation’s values across observations |
| z_ii (Z-score) | The standard deviations recorded which indicates the degree of correlation |
| p_ii (p-value) | The probability of observing the given Moran’s I |
| p_ii_sim (simulated p-value) | The p-value based on the monte carlo simulations |
Weekday Morning Peak Traffic
# Set seed to ensure that results from simulation are reproducible
set.seed(1234)
# Step 1: Merge the data
# Ensure that both wm08 and Origin_6_9 have 'grid_id' as a common key
# and that it's of the same data type in both data frames
merged_data <- wm08 %>%
left_join(origin_6_9, by = "grid_id")
# Step 2: Prepare the data
# Assuming 'area_honeycomb_grid' is the geometry column in wm08
# Convert to an sf object if not already
if (!("sf" %in% class(merged_data))) {
merged_data <- st_as_sf(merged_data, geom_col = "area_honeycomb_grid")
}
# Recreate the neighbor list and spatial weights
# Ensure 'nb' is in the correct format (e.g., created using st_contiguity or similar)
listw <- nb2listw(merged_data$nb, style = "W")
merged_data$standardized_trips <- as.numeric(scale(merged_data$TRIPS, center = TRUE, scale = TRUE))
# Remove NA values from the data
merged_data <- merged_data[!is.na(merged_data$standardized_trips), ]
# Recreate the spatial weights to match the filtered data
listw <- nb2listw(merged_data$nb, style = "W")
# Check if the lengths match
if (nrow(merged_data) != length(listw$neighbours)) {
stop("The length of the data and the spatial weights list do not match.")
}
# Run the Monte Carlo test for Local Moran's
lisa_wd_morn <- merged_data %>%
mutate(local_moran = local_moran(
total_trips, nb, wt, nsim = 99),
.before = 1) %>%
unnest(local_moran)
# unnest the dataframe column
tidyr::unnest(lisa_wd_morn)Simple feature collection with 23878 features and 19 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: 4167.538 ymin: 27151.39 xmax: 46917.54 ymax: 50245.4
Projected CRS: SVY21 / Singapore TM
# A tibble: 23,878 × 20
ii eii var_ii z_ii p_ii p_ii_sim p_folded_sim skewness kurtosis
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.285 -0.00749 0.0694 1.11 0.267 0.02 0.01 -2.06 5.30
2 0.285 -0.00749 0.0694 1.11 0.267 0.02 0.01 -2.06 5.30
3 0.285 -0.00749 0.0694 1.11 0.267 0.02 0.01 -2.06 5.30
4 0.284 0.0734 0.0609 0.852 0.394 0.02 0.01 -2.12 4.77
5 0.284 0.00560 0.312 0.498 0.619 0.06 0.03 -4.62 23.5
6 0.270 0.00300 0.0768 0.962 0.336 0.04 0.02 -3.85 22.0
7 0.270 0.00300 0.0768 0.962 0.336 0.04 0.02 -3.85 22.0
8 0.270 0.00300 0.0768 0.962 0.336 0.04 0.02 -3.85 22.0
9 0.278 0.0170 0.0599 1.07 0.287 0.02 0.01 -2.71 9.88
10 0.278 0.0170 0.0599 1.07 0.287 0.02 0.01 -2.71 9.88
# ℹ 23,868 more rows
# ℹ 11 more variables: mean <fct>, median <fct>, pysal <fct>, wt <dbl>,
# grid_id <int>, total_trips <dbl>, area_honeycomb_grid <POLYGON [m]>,
# nb <int>, BUS_STOP_N <chr>, TRIPS <dbl>, standardized_trips <dbl>Weekday Afternoon/Evening Peak Traffic
Show the code
# Set seed to ensure that results from simulation are reproducible
set.seed(1234)
# Step 1: Merge the data
# Ensure that both wm08 and Origin_6_9 have 'grid_id' as a common key
# and that it's of the same data type in both data frames
merged_data_17_20 <- wm08 %>%
left_join(origin_17_20, by = "grid_id")
# Step 2: Prepare the data
# Assuming 'area_honeycomb_grid' is the geometry column in wm08
# Convert to an sf object if not already
if (!("sf" %in% class(merged_data_17_20))) {
merged_data_17_20 <- st_as_sf(merged_data_17_20, geom_col = "area_honeycomb_grid")
}
# Recreate the neighbor list and spatial weights
# Ensure 'nb' is in the correct format (e.g., created using st_contiguity or similar)
listw <- nb2listw(merged_data_17_20$nb, style = "W")
merged_data_17_20$standardized_trips <- as.numeric(scale(merged_data_17_20$TRIPS, center = TRUE, scale = TRUE))
# Remove NA values from the data
merged_data_17_20 <- merged_data_17_20[!is.na(merged_data_17_20$standardized_trips), ]
# Recreate the spatial weights to match the filtered data
listw <- nb2listw(merged_data_17_20$nb, style = "W")
# Check if the lengths match
if (nrow(merged_data_17_20) != length(listw$neighbours)) {
stop("The length of the data and the spatial weights list do not match.")
}
# Run the Monte Carlo test for Local Moran's
lisa_wd_aft <- merged_data_17_20 %>%
mutate(local_moran = local_moran(
total_trips, nb, wt, nsim = 99),
.before = 1) %>%
unnest(local_moran)
# unnest the dataframe column
tidyr::unnest(lisa_wd_aft)Simple feature collection with 23931 features and 19 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: 4167.538 ymin: 27151.39 xmax: 46917.54 ymax: 50245.4
Projected CRS: SVY21 / Singapore TM
# A tibble: 23,931 × 20
ii eii var_ii z_ii p_ii p_ii_sim p_folded_sim skewness kurtosis
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.284 0.0197 0.0964 0.850 0.395 0.02 0.01 -3.57 16.0
2 0.284 0.0197 0.0964 0.850 0.395 0.02 0.01 -3.57 16.0
3 0.284 0.0197 0.0964 0.850 0.395 0.02 0.01 -3.57 16.0
4 0.283 0.0310 0.161 0.628 0.530 0.04 0.02 -4.53 27.4
5 0.283 0.0399 0.154 0.618 0.537 0.06 0.03 -4.76 30.1
6 0.269 -0.0326 0.249 0.604 0.546 0.04 0.02 -4.29 20.0
7 0.269 -0.0326 0.249 0.604 0.546 0.04 0.02 -4.29 20.0
8 0.269 -0.0326 0.249 0.604 0.546 0.04 0.02 -4.29 20.0
9 0.277 0.00684 0.0737 0.995 0.320 0.02 0.01 -3.22 13.1
10 0.277 0.00684 0.0737 0.995 0.320 0.02 0.01 -3.22 13.1
# ℹ 23,921 more rows
# ℹ 11 more variables: mean <fct>, median <fct>, pysal <fct>, wt <dbl>,
# grid_id <int>, total_trips <dbl>, area_honeycomb_grid <POLYGON [m]>,
# nb <int>, BUS_STOP_N <chr>, TRIPS <dbl>, standardized_trips <dbl>Weekend/Holiday Morning Peak Traffic
Show the code
# Set seed to ensure that results from simulation are reproducible
set.seed(1234)
# Step 1: Merge the data
# Ensure that both wm08 and Origin_6_9 have 'grid_id' as a common key
# and that it's of the same data type in both data frames
merged_data_11_14 <- wm08 %>%
left_join(origin_11_14, by = "grid_id")
# Step 2: Prepare the data
# Assuming 'area_honeycomb_grid' is the geometry column in wm08
# Convert to an sf object if not already
if (!("sf" %in% class(merged_data_11_14))) {
merged_data_11_14 <- st_as_sf(merged_data_11_14, geom_col = "area_honeycomb_grid")
}
# Recreate the neighbor list and spatial weights
# Ensure 'nb' is in the correct format (e.g., created using st_contiguity or similar)
listw <- nb2listw(merged_data_11_14$nb, style = "W")
merged_data_11_14$standardized_trips <- as.numeric(scale(merged_data_11_14$TRIPS, center = TRUE, scale = TRUE))
# Remove NA values from the data
merged_data_11_14 <- merged_data_11_14[!is.na(merged_data_11_14$standardized_trips), ]
# Recreate the spatial weights to match the filtered data
listw <- nb2listw(merged_data_11_14$nb, style = "W")
# Check if the lengths match
if (nrow(merged_data_11_14) != length(listw$neighbours)) {
stop("The length of the data and the spatial weights list do not match.")
}
# Run the Monte Carlo test for Local Moran's
lisa_we_m <- merged_data_11_14 %>%
mutate(local_moran = local_moran(
total_trips, nb, wt, nsim = 99),
.before = 1) %>%
unnest(local_moran)
# unnest the dataframe column
tidyr::unnest(lisa_we_m)Simple feature collection with 23830 features and 19 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: 4167.538 ymin: 27151.39 xmax: 46917.54 ymax: 50245.4
Projected CRS: SVY21 / Singapore TM
# A tibble: 23,830 × 20
ii eii var_ii z_ii p_ii p_ii_sim p_folded_sim skewness kurtosis
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.285 -0.0458 0.154 0.845 0.398 0.02 0.01 -2.90 10.4
2 0.285 -0.0458 0.154 0.845 0.398 0.02 0.01 -2.90 10.4
3 0.285 -0.0458 0.154 0.845 0.398 0.02 0.01 -2.90 10.4
4 0.284 0.0145 0.237 0.554 0.579 0.04 0.02 -4.81 26.3
5 0.284 0.0439 0.0833 0.833 0.405 0.02 0.01 -2.43 6.68
6 0.270 0.0165 0.0608 1.03 0.303 0.04 0.02 -2.18 5.62
7 0.270 0.0165 0.0608 1.03 0.303 0.04 0.02 -2.18 5.62
8 0.270 0.0165 0.0608 1.03 0.303 0.04 0.02 -2.18 5.62
9 0.278 -0.0252 0.0940 0.990 0.322 0.02 0.01 -2.44 6.09
10 0.278 -0.0252 0.0940 0.990 0.322 0.02 0.01 -2.44 6.09
# ℹ 23,820 more rows
# ℹ 11 more variables: mean <fct>, median <fct>, pysal <fct>, wt <dbl>,
# grid_id <int>, total_trips <dbl>, area_honeycomb_grid <POLYGON [m]>,
# nb <int>, BUS_STOP_N <chr>, TRIPS <dbl>, standardized_trips <dbl>Weekend/Holiday Evening Peak Traffic
Show the code
# Set seed to ensure that results from simulation are reproducible
set.seed(1234)
# Step 1: Merge the data
# Ensure that both wm08 and Origin_6_9 have 'grid_id' as a common key
# and that it's of the same data type in both data frames
merged_data_16_19 <- wm08 %>%
left_join(origin_16_19, by = "grid_id")
# Step 2: Prepare the data
# Assuming 'area_honeycomb_grid' is the geometry column in wm08
# Convert to an sf object if not already
if (!("sf" %in% class(merged_data_16_19))) {
merged_data_16_19 <- st_as_sf(merged_data_16_19, geom_col = "area_honeycomb_grid")
}
# Recreate the neighbor list and spatial weights
# Ensure 'nb' is in the correct format (e.g., created using st_contiguity or similar)
listw <- nb2listw(merged_data_16_19$nb, style = "W")
merged_data_16_19$standardized_trips <- as.numeric(scale(merged_data_16_19$TRIPS, center = TRUE, scale = TRUE))
# Remove NA values from the data
merged_data_16_19 <- merged_data_16_19[!is.na(merged_data_16_19$standardized_trips), ]
# Recreate the spatial weights to match the filtered data
listw <- nb2listw(merged_data_16_19$nb, style = "W")
# Check if the lengths match
if (nrow(merged_data_16_19) != length(listw$neighbours)) {
stop("The length of the data and the spatial weights list do not match.")
}
# Run the Monte Carlo test for Local Moran's
lisa_we_e <- merged_data_16_19 %>%
mutate(local_moran = local_moran(
total_trips, nb, wt, nsim = 99),
.before = 1) %>%
unnest(local_moran)
# unnest the dataframe column
tidyr::unnest(lisa_we_e)Simple feature collection with 23843 features and 19 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: 4167.538 ymin: 27151.39 xmax: 46917.54 ymax: 50245.4
Projected CRS: SVY21 / Singapore TM
# A tibble: 23,843 × 20
ii eii var_ii z_ii p_ii p_ii_sim p_folded_sim skewness kurtosis
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.285 0.0391 0.0355 1.31 0.192 0.02 0.01 -1.56 2.78
2 0.285 0.0391 0.0355 1.31 0.192 0.02 0.01 -1.56 2.78
3 0.285 0.0391 0.0355 1.31 0.192 0.02 0.01 -1.56 2.78
4 0.284 0.0645 0.0767 0.793 0.428 0.12 0.06 -2.68 10.2
5 0.284 0.0481 0.0861 0.804 0.421 0.1 0.05 -3.32 14.7
6 0.270 -0.0307 0.0930 0.986 0.324 0.04 0.02 -2.86 11.5
7 0.270 -0.0307 0.0930 0.986 0.324 0.04 0.02 -2.86 11.5
8 0.270 -0.0307 0.0930 0.986 0.324 0.04 0.02 -2.86 11.5
9 0.278 0.0350 0.0613 0.982 0.326 0.02 0.01 -2.95 10.9
10 0.278 0.0350 0.0613 0.982 0.326 0.02 0.01 -2.95 10.9
# ℹ 23,833 more rows
# ℹ 11 more variables: mean <fct>, median <fct>, pysal <fct>, wt <dbl>,
# grid_id <int>, total_trips <dbl>, area_honeycomb_grid <POLYGON [m]>,
# nb <int>, BUS_STOP_N <chr>, TRIPS <dbl>, standardized_trips <dbl># Example of a how we derive Moran I and a Simulated Moran I P value for a Weekday Morning.
# Set map to static
tmap_mode("plot")
# Weekday Morning Moran I value
map_wdm_moran08 <- tm_shape(lisa_wd_morn) +
tm_fill(
col = "ii",
palette = "OrRd",
style = "pretty",
title = "Local Moran's I"
) +
tm_layout(main.title = "Weekday Morning Peak Traffic",
main.title.size = 1,
main.title.position = "center",
legend.position = c("left", "top"),
legend.height = .6,
legend.width = .2,
frame = FALSE
)
# Moran I Simulated P value
map_wdm_moran08_p <- tm_shape(lisa_wd_morn) +
tm_fill(
col = "p_ii_sim",
palette = "BuGn",
style = "pretty",
title = "Simulated P value"
) +
tm_layout(
main.title.size = 1,
main.title.position = "center",
legend.position = c("left", "top"),
legend.height = .6,
legend.width = .2,
frame = FALSE
)Show the code
# Weekday Afternoon Moran I
map_wda_moran08 <- tm_shape(lisa_wd_aft) +
tm_fill(
col = "ii",
palette = "OrRd",
style = "pretty",
title = "Local Moran's I"
) +
tm_layout(main.title = "Weekday Afternoon Peak Traffic",
main.title.size = 1,
main.title.position = "center",
legend.position = c("left", "top"),
legend.height = .6,
legend.width = .2,
frame = FALSE
)
# Moran I Simulated P value
map_wda_moran08_p <- tm_shape(lisa_wd_aft) +
tm_fill(
col = "p_ii_sim",
palette = "BuGn",
style = "pretty",
title = "Simulated P value"
) +
tm_layout(
main.title.size = 1,
main.title.position = "center",
legend.position = c("left", "top"),
legend.height = .6,
legend.width = .2,
frame = FALSE
)
# Weekend/Holiday Morning Moran I
map_we_moran08 <- tm_shape(lisa_we_m) +
tm_fill(
col = "ii",
palette = "PuRd",
style = "pretty",
title = "Local Moran's I"
) +
tm_layout(main.title = "Weekend Morning Peak Traffic",
main.title.size = 1,
main.title.position = "center",
legend.position = c("left", "top"),
legend.height = .6,
legend.width = .2,
frame = FALSE
)
# Moran I Simulated P value
map_we_moran08_p <- tm_shape(lisa_we_m) +
tm_fill(
col = "p_ii_sim",
palette = "BuGn",
style = "pretty",
title = "Simulated P value"
) +
tm_layout(
main.title.size = 1,
main.title.position = "center",
legend.position = c("left", "top"),
legend.height = .6,
legend.width = .2,
frame = FALSE
)
# Weekend/Holiday Evening Moran I
map_wa_moran08 <- tm_shape(lisa_we_e) +
tm_fill(
col = "ii",
palette = "PuRd",
style = "pretty",
title = "Local Moran's I"
) +
tm_layout(main.title = "Weekend Afternoon Peak Traffic",
main.title.size = 1,
main.title.position = "center",
legend.position = c("left", "top"),
legend.height = .6,
legend.width = .2,
frame = FALSE
)
# Moran I Simulated P value
map_wa_moran08_p <- tm_shape(lisa_we_e) +
tm_fill(
col = "p_ii_sim",
palette = "BuGn",
style = "pretty",
title = "Simulated P value"
) +
tm_layout(
main.title.size = 1,
main.title.position = "center",
legend.position = c("left", "top"),
legend.height = .6,
legend.width = .2,
frame = FALSE
)tmap_arrange(map_wdm_moran08, map_wa_moran08,
map_wdm_moran08_p, map_wa_moran08_p,
map_wda_moran08, map_we_moran08,
map_wda_moran08_p, map_we_moran08_p,
ncol = 2)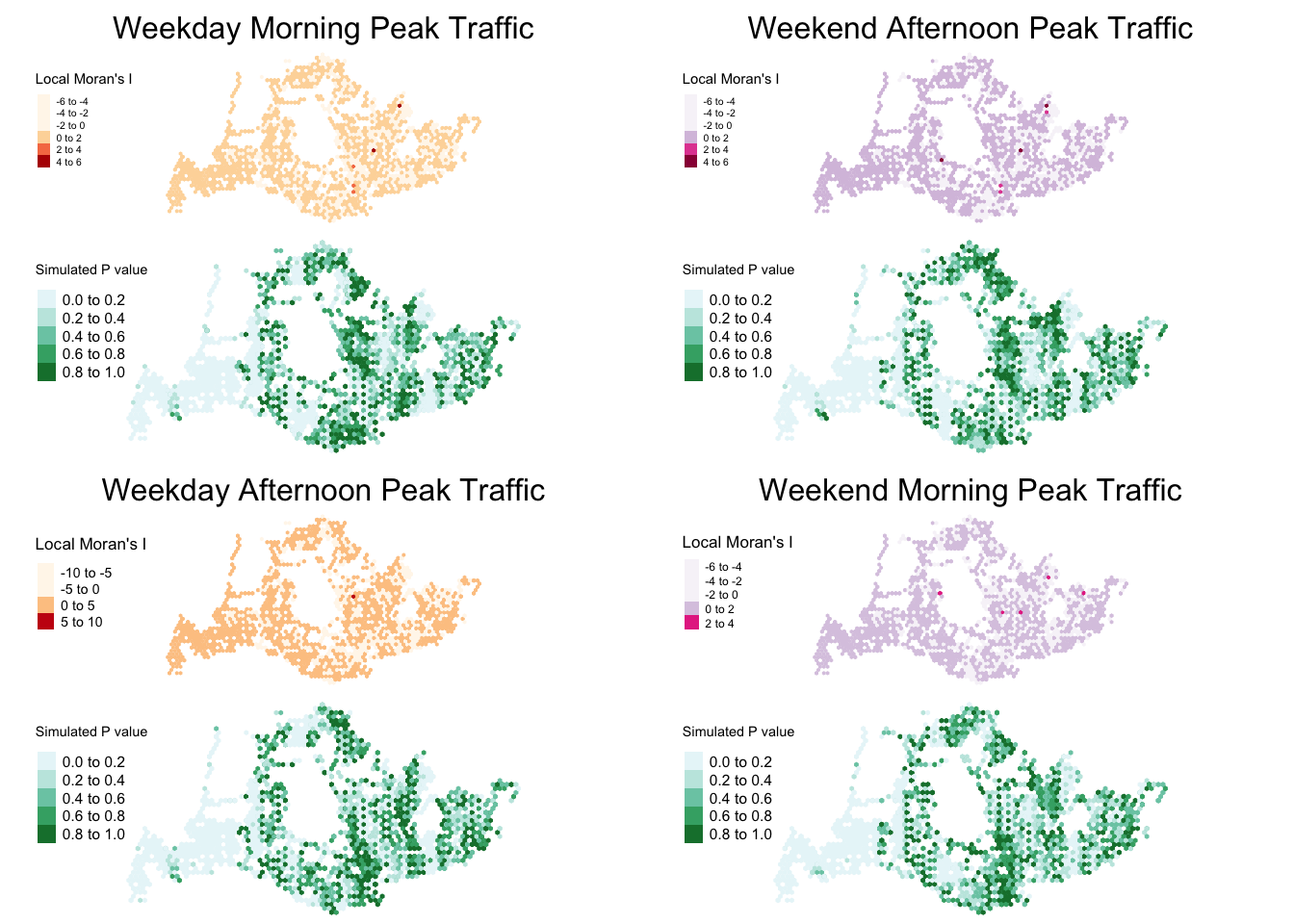
Step 5: Concluding our findings
From both a visual and data analysis angle, we can see that there are significant clusters forming in parts of Singapore especially during weekday mornings. To visualise these clusterings, we will proceed to look at the mean value derived from our Local_Moran function for the different time spaces.
Visualizing Clusters < 0.05 p value
The spatial clusters are visualize in the maps below with one showing all values and the others displaying only statistically significant clusters (p-value <0.05) with both simulated and non simulated data:
tmap_mode("plot")
plot_wdm_all <-
tm_shape(lisa_wd_morn) +
tm_fill(
col = "mean",
style = "cat",
palette = "Spectral"
) +
tm_layout(
main.title = "Map A: Local Moran Clusters",
main.title.size = 1,
main.title.position = "center",
frame = FALSE)
mean_wdm <- lisa_wd_morn %>%
filter(p_ii <= 0.05)
mean_wd_sim <- lisa_wd_morn %>%
filter(p_ii_sim <= 0.05)
plot_wdm_mean <-
tm_shape(lisa_wd_morn) +
tm_polygons(
col = "#ffffff"
) +
tm_borders(col = NA) +
tm_shape(mean_wdm) +
tm_fill(
col = "mean",
style = "cat",
palette = "PuRd"
) +
tm_layout(
main.title = "Map B: Local Moran Clusters (P value is 0.05 or lesser)",
main.title.size = 1,
main.title.position = "center",
frame = FALSE)
plot_wdm_mean_sim <-
tm_shape(lisa_wd_morn) +
tm_polygons(
col = "#ffffff"
) +
tm_borders(col = NA) +
tm_shape(mean_wd_sim) +
tm_fill(
col = "mean",
style = "cat",
palette = "PuRd"
) +
tm_layout(
main.title = "Map C: Local Moran Clusters Simulated (P value is 0.05 or lesser)",
main.title.size = 1,
main.title.position = "center",
frame = FALSE)
plot_wdm_all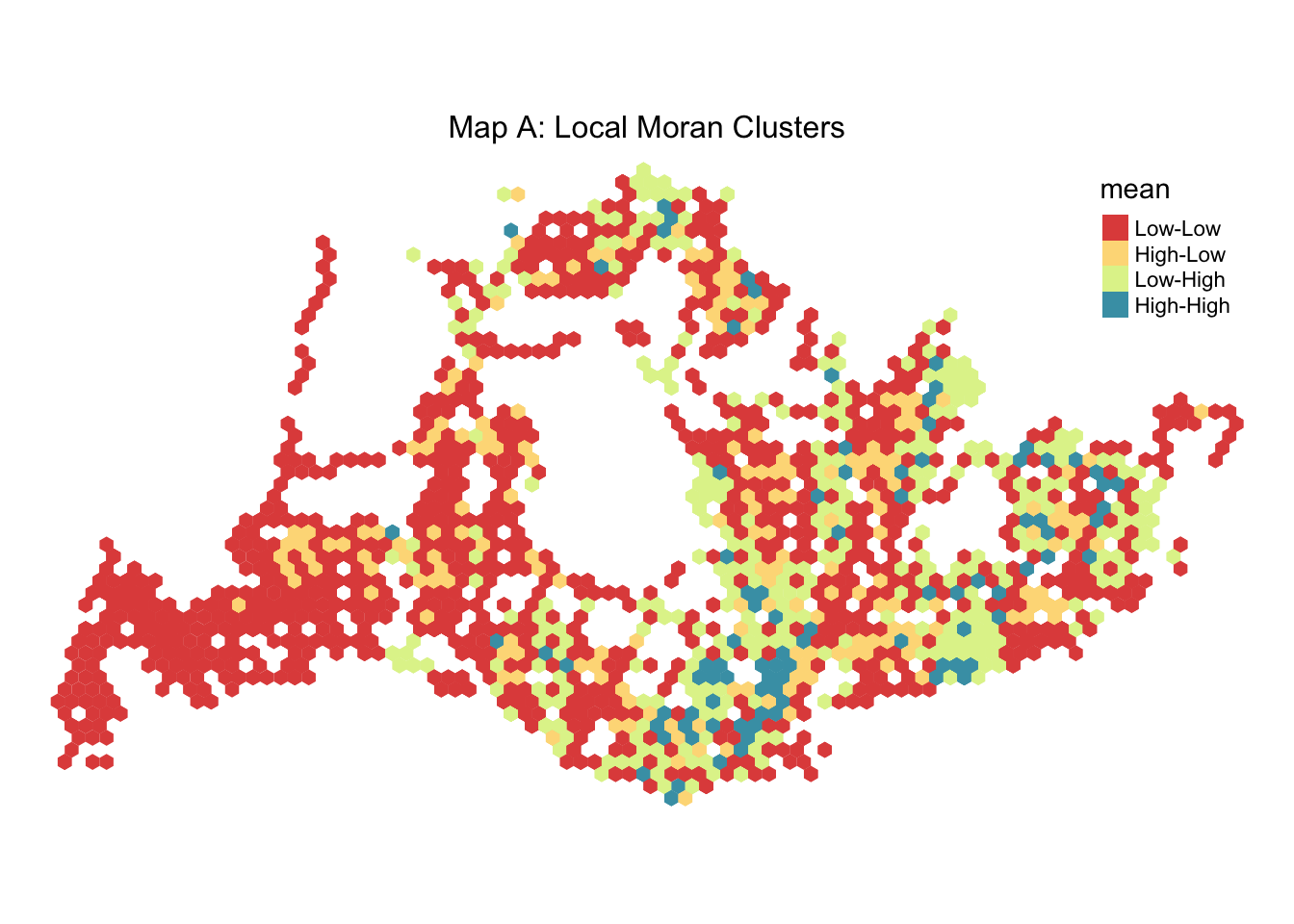
tmap_arrange(plot_wdm_mean,plot_wdm_mean_sim ,
ncol = 2)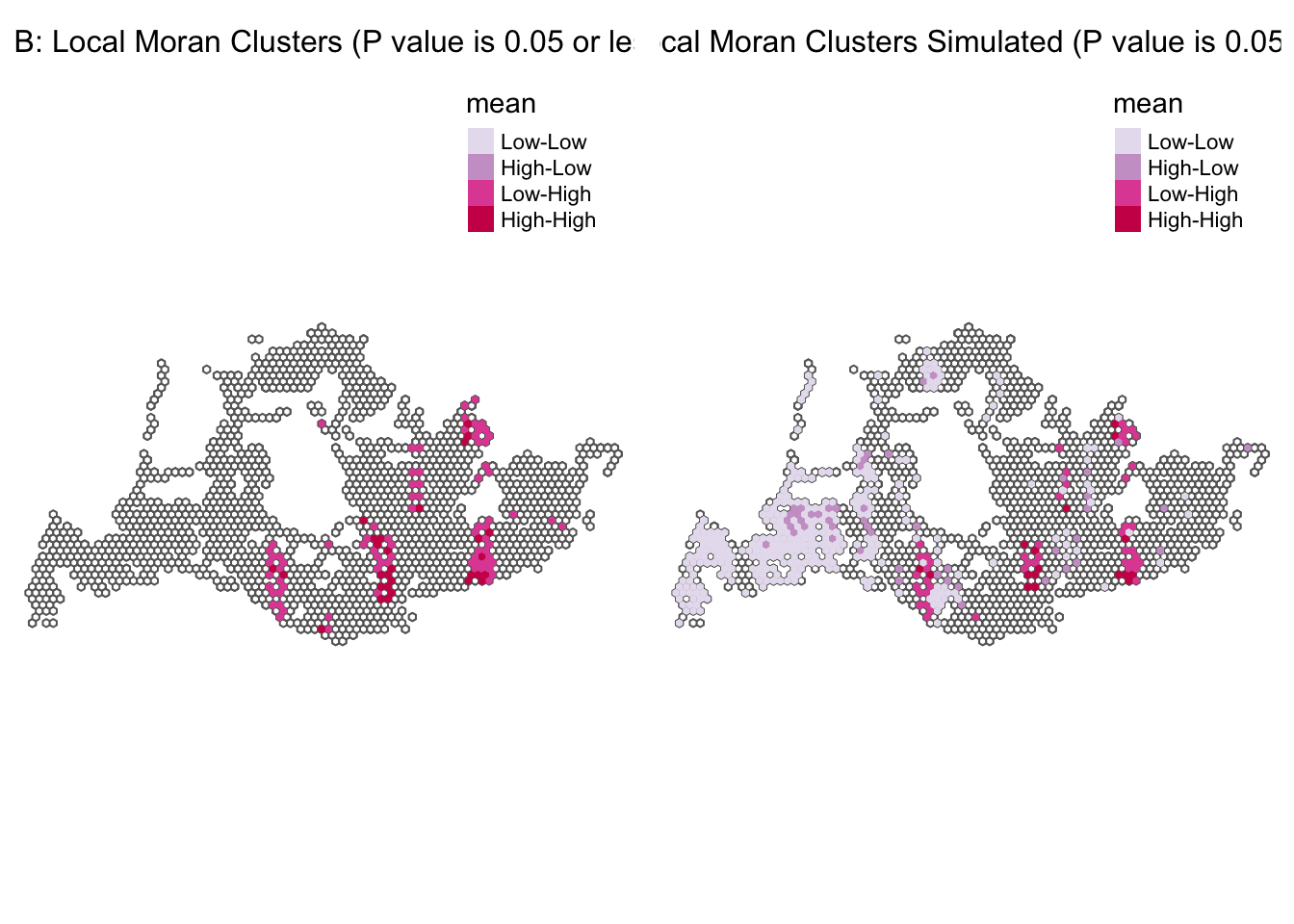
Summary
We have two maps labeled “Map B: Local Moran Clusters Simulated” and “Map C: Local Moran Clusters” both with a p-value of 0.05 or less indicating statistically significant spatial clusters the data.
Map B shows actual observed data with similar clusters: - Low-Low areas appear more dispersed, suggesting pockets of low demand spread throughout the region. - High-Low areas are also present but less prevalent than in the simulated map. - Pink areas (Low-High) are not present, indicating no significant points with low traffic surrounded by high traffic areas. - Red areas (High-High) represent highly trafficked stops in areas that also have high traffic, possibly central city locations or busy corridors.
Map C (“Simulated”) represents a simulated scenario:
- Light Purple (Low-Low): Areas with lower than average bus traffic that are surrounded by areas with similarly low traffic, suggesting regions of uniformly low demand or service.
- Dark Purple (High-Low): These spots indicate bus stops with high traffic that are not surrounded by similarly high-traffic areas, which could represent major transit hubs or end-of-line stops.